
Understanding Matrix Factorization

Pseudo code for SGD and CCD algorithm:
SGD

CCD

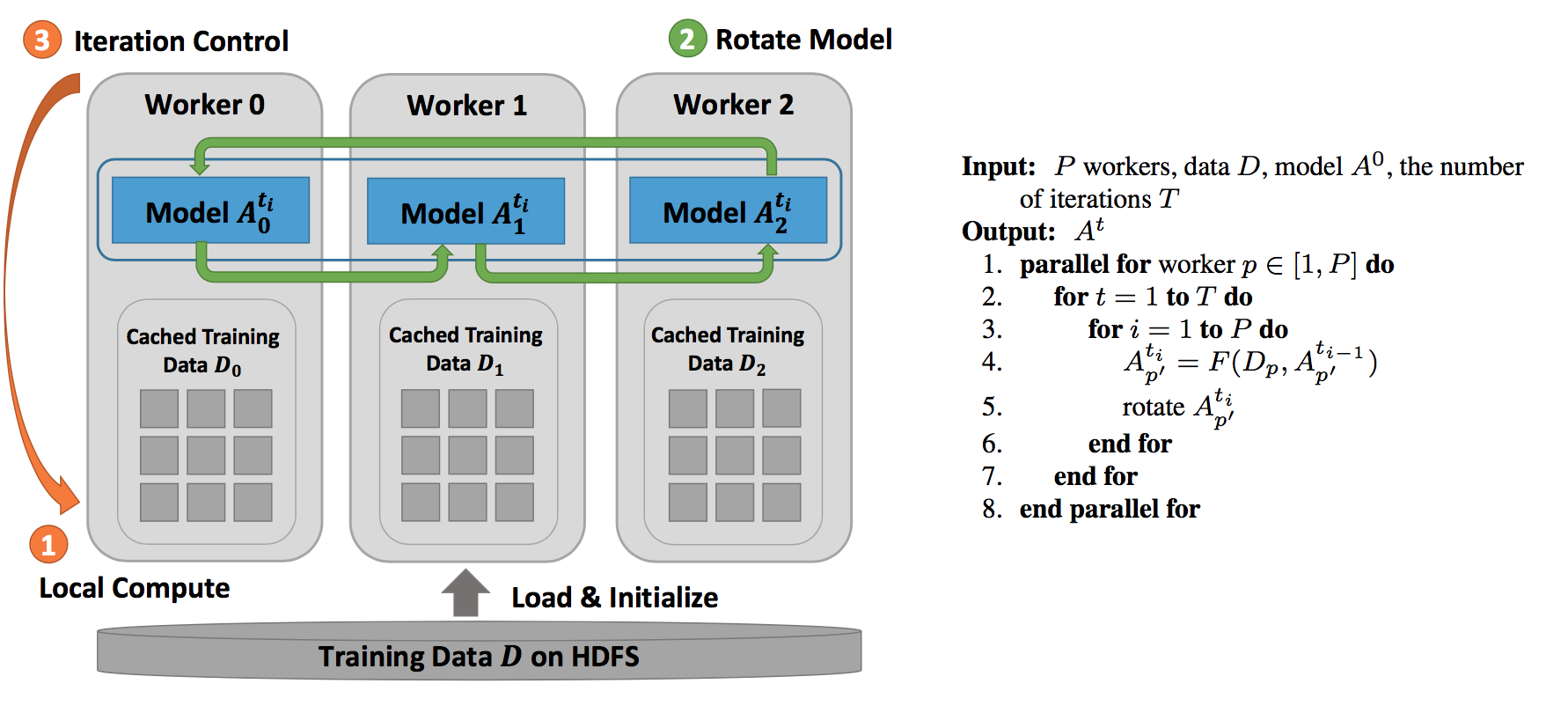
Using Model Rotation to parallel MF algorithms
Model rotation is expressed as a collective communication. The operation takes the model part owned by a process and performs the rotation. By default, the operation sends the model partitions to the next neighbor and receives the model partitions from the last neighbor in a predefined ring topology of workers. An advanced option is that the ring topology can be dynamically defined before performing the model rotation. Thus, programming model rotation requires just one API. For local computations inside each worker, they are simply programmed through an interface of “schedule-update”. A scheduler employs a user-defined function to maintain a dynamic order of model parameter updates and avoid the update conflict. Since the local computation only needs to process the model obtained during the rotation without considering the parallel model updates from other workers, the code of a parallel machine learning algorithm can be modularized as a process of performing computation and rotating model partitions.
We adopt Model Rotation to parallel SGD and CCD algorithms. The data flow and algorithm are shown as follows:
Performance
|
|

Experiments are conducted on a 128-node Intel Haswell cluster at Indiana University. Among them, 32 nodes each have two 18-core Xeon E5-2699 v3 processors (36 cores in total), and 96 nodes each have two 12-core Xeon E5- 2670 v3 processors (24 cores in total). All the nodes have 128 GB memory and are connected by QDR InfiniBand. For our tests, JVM memory is set to “-Xmx120000m -Xms120000m”, and IPoIB is used for communication.
We use one big dataset which is generated from “ClueWeb09” to test LDA both on Harp and Petuum.
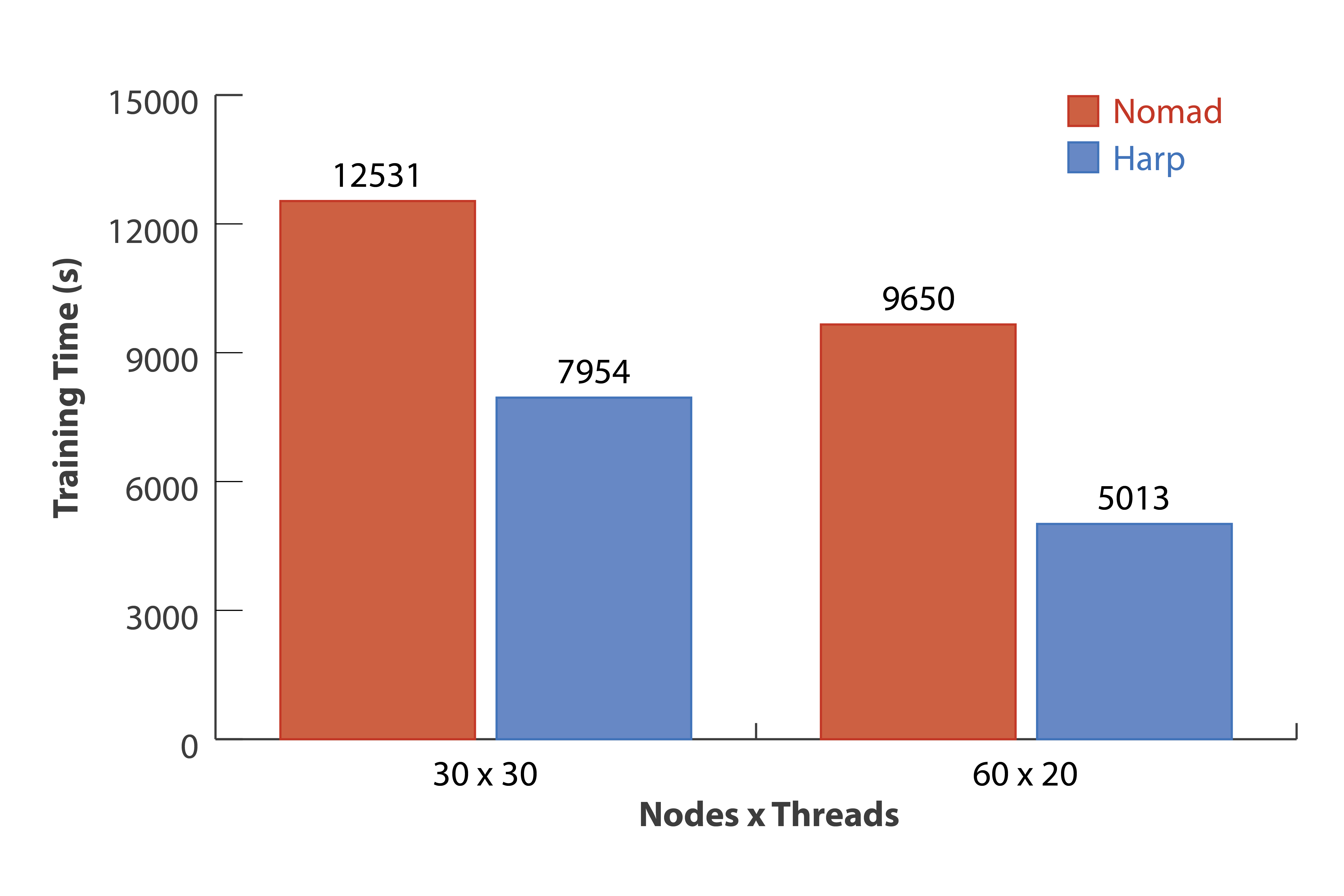
In SGD, Harp SGD converges faster than NOMAD. On “clueweb2”, with 30 nodes × 30 threads Xeon E5-2699 v3 nodes, Harp is 58% faster, and with 60 nodes × 20 threads Xeon E5-2670 v3 nodes, Harp is 93% faster when the test RMSE value converges to 1.61. The difference of the convergence speed increases because the random shifting mechanism in NOMAD becomes unstable when the scale goes up.
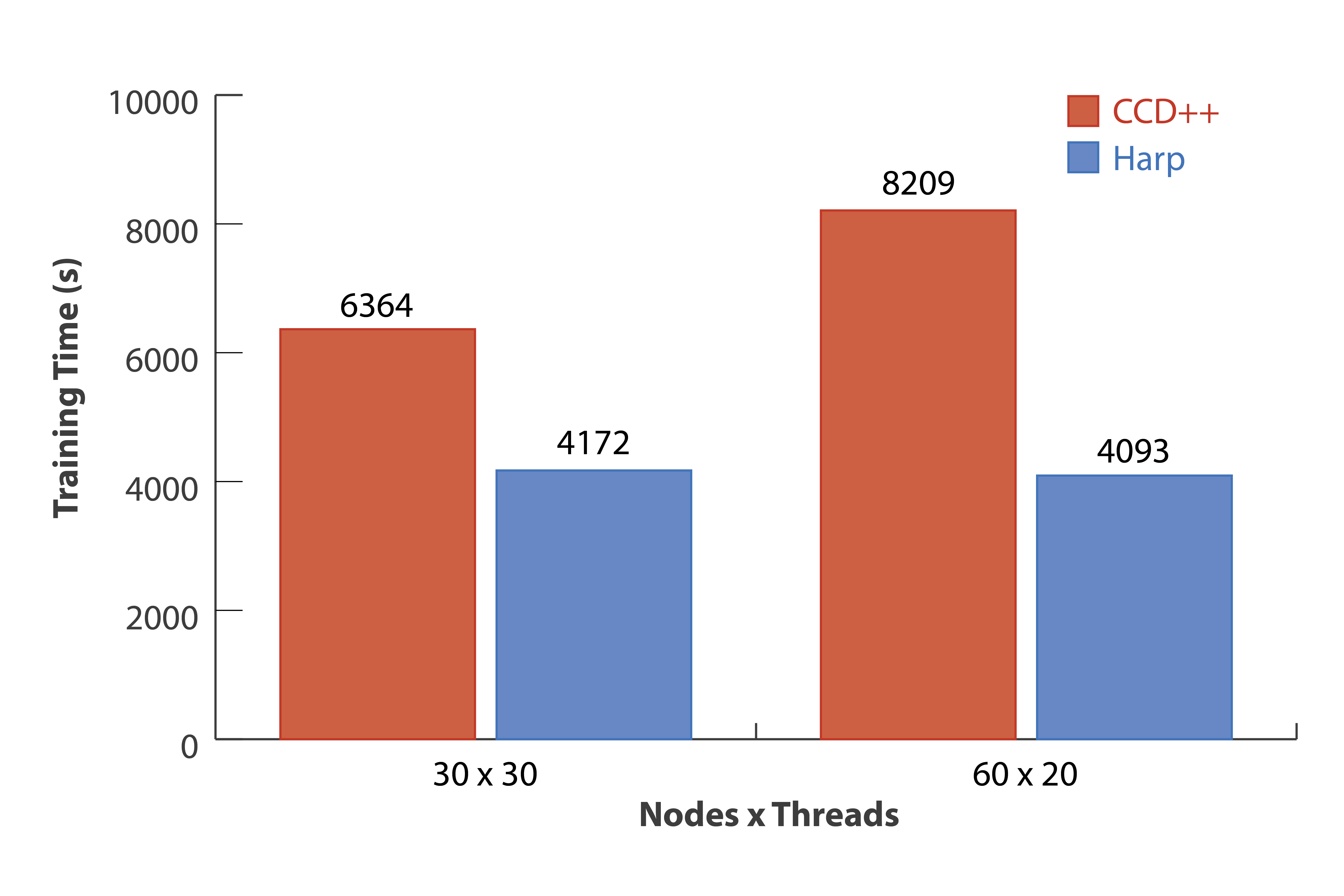
In CCD, we again test the model convergence speed on “clueweb2” dataset. The results show that Harp CCD also has comparable performance with CCD++. Note that CCD++ use a different model update order so that the convergence rate based on the same number of model update count is different with Harp CCD. However, the tests on “clueweb2” reveal that with 30 nodes × 30 threads Xeon E5-2670 v3 nodes Harp CCD is 53% faster than CCD++ and with 60 nodes × 20 threads Xeon E5-2699 v3 nodes Harp CCD is 101% faster than CCD++ when the test RMSE converges to 1.68.
Run SGD and CCD example
Data
You can download public data and transfer to the data format required by sgd and ccd application. Here are some datasets for your reference.
Data Format
The format for the data should be a list of <userid, itemid, rating> in the case of a recommendation system.
For example,
1 4026 3.299341
1 5990 7.005311
2 5988 13.235623
2 346 3.518781
3 347 2.846904
Usage
SGD
hadoop jar harp-java-0.1.0.jar edu.iu.sgd.SGDLauncher <input dir> <r> <lambda> <epsilon> <num of iterations> <training ratio> <num of map tasks> <num of threads per worker> <schedule ratio><memory (MB)> <work dir> <test dir>
<input dir> ; input directory
<r> <lambda> <epsilon> ; hyper-parameters, different for different datasets
<num of iterations> ; iteratoin number
<training ratio> ; set the percentage of training to utilize timer control of synchronization
<num of map tasks> ;
<num of threads per worker> ;
<schedule ratio> ; blocks partition ratio for dynamic scheduler, 2 means spliting to 2xThread# X 2xMapper# blocks
<memory (MB)> ; memory setting for JVM
<work dir> ; working directory, model saved in this directory
<test dir> ; directory for test files
Example
#put data onto hdfs
cp $HARP_ROOT_DIR/datasets/tutorial/movielens/* .
bunzip2 movie*.mm.bz2
mkdir data
cd data/
split -a 5 -l 10000 ../movielens-train.mm
cd ..
hadoop fs -mkdir -p /harp-test/mf/test
hadoop fs -put data /harp-test/mf/
hadoop fs -put movielens-test.mm /harp-test/mf/test
#run lda training
hadoop jar harp-java-0.1.0.jar edu.iu.sgd.SGDLauncher /harp-test/mf/data 40 0.05 0.003 100 100 10 16 2 10000 /harp-test/mfwork/ /harp-test/mf/test/
### CCD
```bash
hadoop jar harp-java-0.1.0.jar edu.iu.ccd.CCDLauncher <input dir> <r> <lambda> <num of iterations> <num of map tasks> <num of threads per worker> <num of model slices> <work dir> <test dir>