Before going through this tutorial take a look at the overview section to get an understanding of the structure of the tutorial.
Definitions:
Nis the number of data pointsTis the number of labelsMis the number of featuresWis theT*Mweight matrixKis the number of iteration
Multiclass logistic regression (MLR) is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than two possible discrete outcomes. It is a model that is used to predict the probabilities of the different possible outcomes of a categorically distributed dependent variable, given a set of independent variables.
The process of the MLR algorithm is:
Use the weight
Wto predict the label of current data point.Compare the output and the answer.
Use SGD to approximate
W.Repeat step 1 to 3 with each label and their weights.
Stochastic gradient descent (SGD) is a stochastic approximation of the gradient descent optimization method for minimizing an objective function that is written as the sum of differentiable functions. In other words, SGD tries to find minimums or maximums by iteration. As the algorithm sweeps through the training set, it performs the update for each training example. Several passes can be made over the training set until the algorithm converges.
The SGD algorithm can be described as following:
Randomly assign the weight
W.Shuffle
Ndata points.Go through
Ndata points and do gradient descent.Repeat step 2 and 3
Ktimes.
PARALLEL DESIGN
What are the models? What kind of data structure is applicable?
The weight vectors for classes are models. Because an ovr(one-versus-rest) approach is adopted, each weight vector is independent. It has a matrix structure.
What are the characteristics of the data dependency in model update computation? Can updates run concurrently?
Model update computation here is the SGD update, in which for each data point it should update the model directly. Because of the ovr strategy, each row in the model matrix is independent, and can be updated in parallel.
Which kind of parallelism scheme is suitable, data parallelism or model parallelism?
Data parallelism can be used, i.e., calculating different data points in parallel.
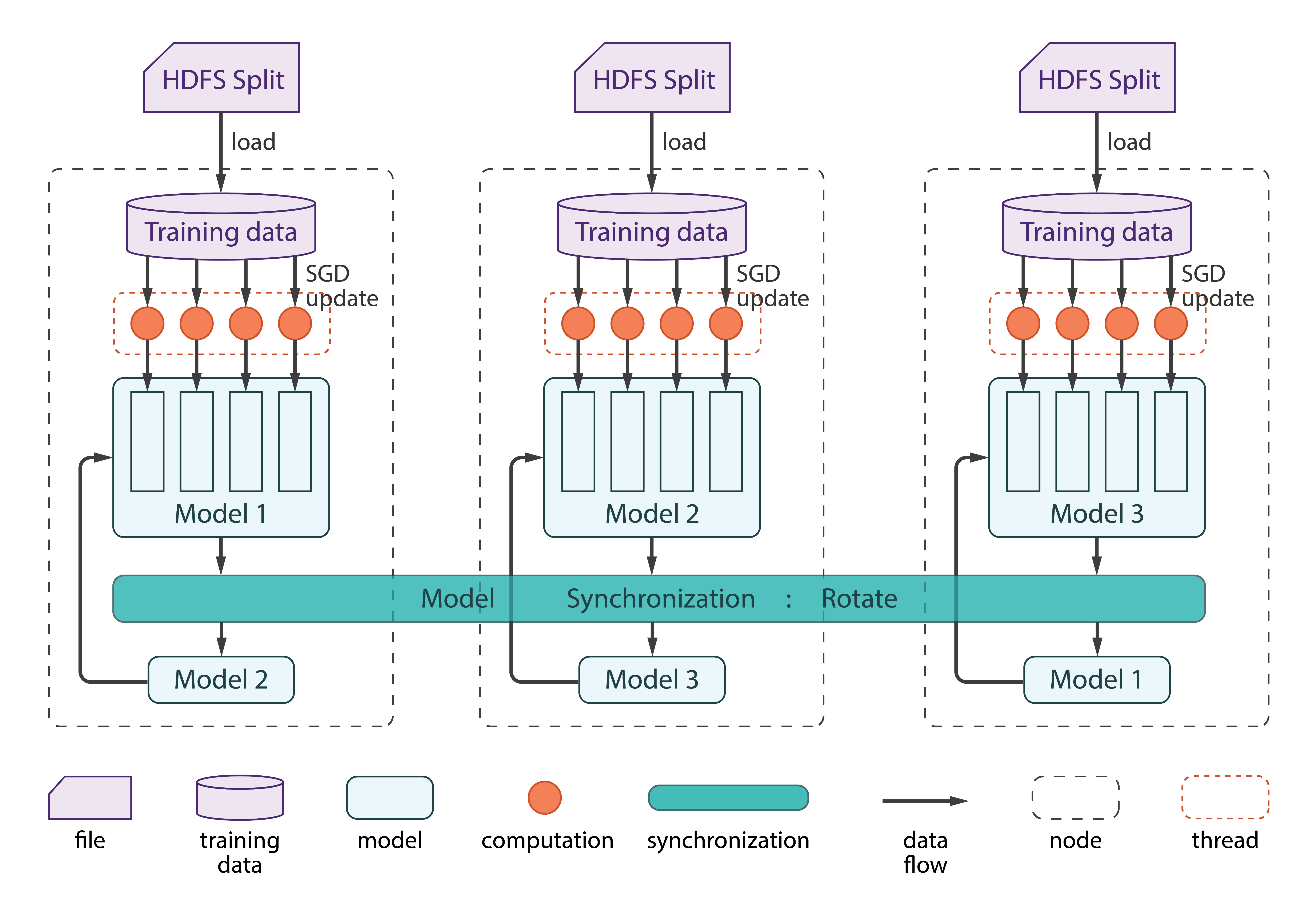
Because the updates can run concurrently, model parallelism is a nature solution. Each node gets one partition of the model, which updates in parallel. And furthermore, thread level parallelism can also follow this model parallelism pattern, that each thread takes a subset of partition and updates in parallel independently.
Which collective communication operation is suitable to synchronize the model?
DynamicScheduler can be used for thread-level parallelism, and Rotate can be used in the inter-node model synchronization.
DATAFLOW
Step 0 — Data preprocessing
Harp MLR will use the data in the vector format. Each vector in a file is represented by the format <did> [<fid>:<weight>]:
<did>is an unique document id<fid>is a positive feature id<weight>is the number feature value within document weight
After preprocessing, push the data set into HDFS by the following commands.
hdfs dfs -mkdir /input
hdfs dfs -put input_data/* /input
Step 1 — Initialize
For Harp MLR, we will use dynamic scheduling as mentioned above. Before we set up the dynamic scheduler, we need to initialize the weight matrix W, which will be partitioned into T parts representing to T labels which means that each label belongs to one partition and is treated as an independent task.
private void initTable() {
wTable = new Table(0, new DoubleArrPlus());
for (int i = 0; i < topics.size(); i++)
wTable.addPartition(new Partition(i, DoubleArray.create(TERM + 1, false)));
}
After that, we can initialize the dynamic scheduler. Each thread will be treated as a worker and will be added into the scheduler. The only thing that needs to be done is that tasks have to be submitted during the computation.
private void initThread() {
GDthread = new LinkedList<>();
for (int i = 0; i < numThread; i++)
GDthread.add(new GDtask(alpha, data, topics, qrels));
GDsch = new DynamicScheduler<>(GDthread);
}
Step 2 — Mapper communication
In this main process, we use regroup to distribute the partitions to the workers first. The workers will get almost the same number of partitions. Then we start the scheduler. Each time we submit one partition to each thread in the scheduler, the threads will all use SGD to approximate W with each label. After the workers finish once with their own partitions, we will use rotate operation to swap the partitions among the workers. After all the processes finish, each worker should use its own data training the whole partition K times, where K is the number of iterations. allgather operation collects all partitions in each worker, combines the partitions, and shares the outcome with all workers. Finally, the Master worker outputs the weight matrix W.
protected void mapCollective(KeyValReader reader, Context context) throws IOException, InterruptedException {
LoadAll(reader);
initTable();
initThread();
regroup("MLR", "regroup_wTable", wTable, new Partitioner(getNumWorkers()));
GDsch.start();
for (int iter = 0; iter < ITER * numMapTask; iter++) {
for (Partition par : wTable.getPartitions())
GDsch.submit(par);
while (GDsch.hasOutput())
GDsch.waitForOutput();
rotate("MLR", "rotate_" + iter, wTable, null);
context.progress();
}
GDsch.stop();
allgather("MLR", "allgather_wTable", wTable);
if (isMaster())
Util.outputData(outputPath, topics, wTable, conf);
wTable.release();
}
Data
The dataset used is the (RCV1-v2)[http://www.ai.mit.edu/projects/jmlr/papers/volume5/lewis04a/lyrl2004_rcv1v2_README.htm] dataset.
Run example
Compile
Select the profile related to your hadoop version. For ex: hadoop-2.6.0. Supported hadoop versions are 2.6.0, 2.7.5 and 2.9.0
cd $HARP_ROOT_DIR
mvn clean package -Phadoop-2.6.0
cd $HARP_ROOT_DIR/contrib/target
cp contrib-0.1.0.jar $HADOOP_HOME
cd $HADOOP_HOME
Put data on hdfs
hdfs dfs -mkdir /rcv1v2
rm -rf data
mkdir -p data
cd data
split -l 1000 $HARP_ROOT_DIR/datasets/tutorial/rcv1/lyrl2004_vectors_train.dat
cd ..
hdfs dfs -put data /rcv1v2
hdfs dfs -put $HARP_ROOT_DIR/datasets/tutorial/rcv1/rcv1* /rcv1v2
Run
hadoop jar contrib-0.1.0.jar edu.iu.mlr.MLRMapCollective [alpha] [number of iteration] [number of features] [number of workers] [number of threads] [topic file path] [qrel file path] [input path in HDFS] [output path in HDFS]
Example
hadoop jar contrib-0.1.0.jar edu.iu.mlr.MLRMapCollective 1.0 100 47236 2 4 /rcv1v2/rcv1.topics.txt /rcv1v2/rcv1-v2.topics.qrels /rcv1v2 /output
The output should be the weight matrix W.
Please refer to the test scripts (mlr.sh) under test_scripts for more details.