Overview
What is Subgraph Counting?
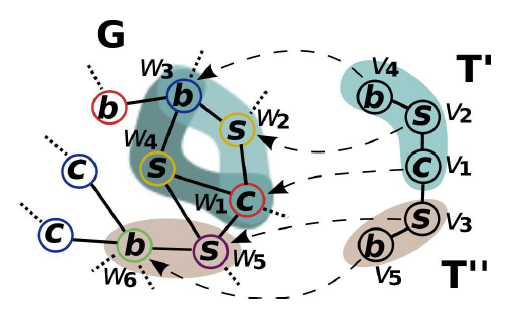
Subgraph counting goes under many names such as template matching or motif counting, but they all generally refer to counting the amount of a template T, that are present in a graph G. Refering to our illustration above, we may imagine that the template T (Here T is split on T’ and T”) on the right could fit in graph G in a few ways right? Well we would like to quantify just how many times T can fit in G. Such general problem manifests itself in many domains such as genomics, design of electronic circuits, and social network analysis.
How do we solve this problem?
We use the Color-coding approximation formulated by (Alon et. al., 1995) which can be presented the following way:
1. Establish a group of k distinct colors, where k is the number of vertices in the template T
2. Randomly color each vertex of graph G with the k distinct colors
3. Count all colorful (meaning all vertices have a distinct color with no duplicates) copies of T in G rooted at every vertex v using
the following formula and diagram, where this is achieved by bottom-up dynamic programming. This means that we start by counting
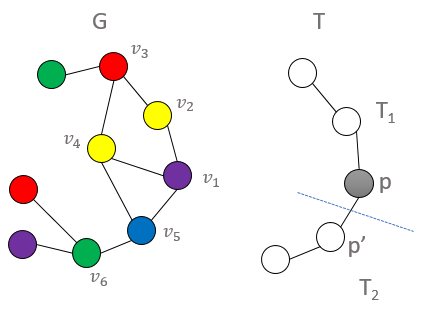
the colorful copies of each one vertex tuple (this is trivial as they are all one distinct color), then we buid up to two vertex
tuples and use the counts of the previous one-tuple step where we have the notion of an active child p, and a passive child p’.
Thus, we count all two-tuple embeddings where p is rooted at some vertex v in G, and p’ is its adjacent neighbor, then we multiply
their colorful combinations. We continue this process for 3-tuples by using the 2-tuple and 1-tuple counts, and finally we conclude
by finding the 5-tuple (final template count) by using the 3-tuple and 2-tuple counts. As a last counting step, we divide by d, where d is equal
to one plus the number of siblings of p’ which are roots of subtrees isomorphic to the subtemplate
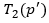
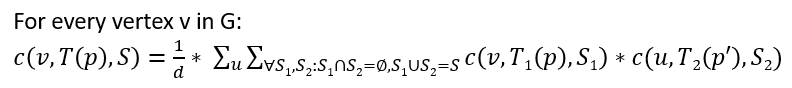 4. Sum up the template counts at all the vertices, then divide by q (which signifies the possibility of the template T being isomorphic to itself) as the following:
4. Sum up the template counts at all the vertices, then divide by q (which signifies the possibility of the template T being isomorphic to itself) as the following:
 5. Multiply the final sum N by the probability of any given template T to be colorful as the following:
5. Multiply the final sum N by the probability of any given template T to be colorful as the following:
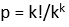 6. If needed, repeat this process more times and average the count to obtain a more accurate measure (as this method yields an approximation)
6. If needed, repeat this process more times and average the count to obtain a more accurate measure (as this method yields an approximation)
Implementation
Node-level Communication
Harp-DAAL-Subgraph uses a unique Adaptive-Group Communication approach for its node-level (process) communication based upon the collective regroup operation provided by Harp,
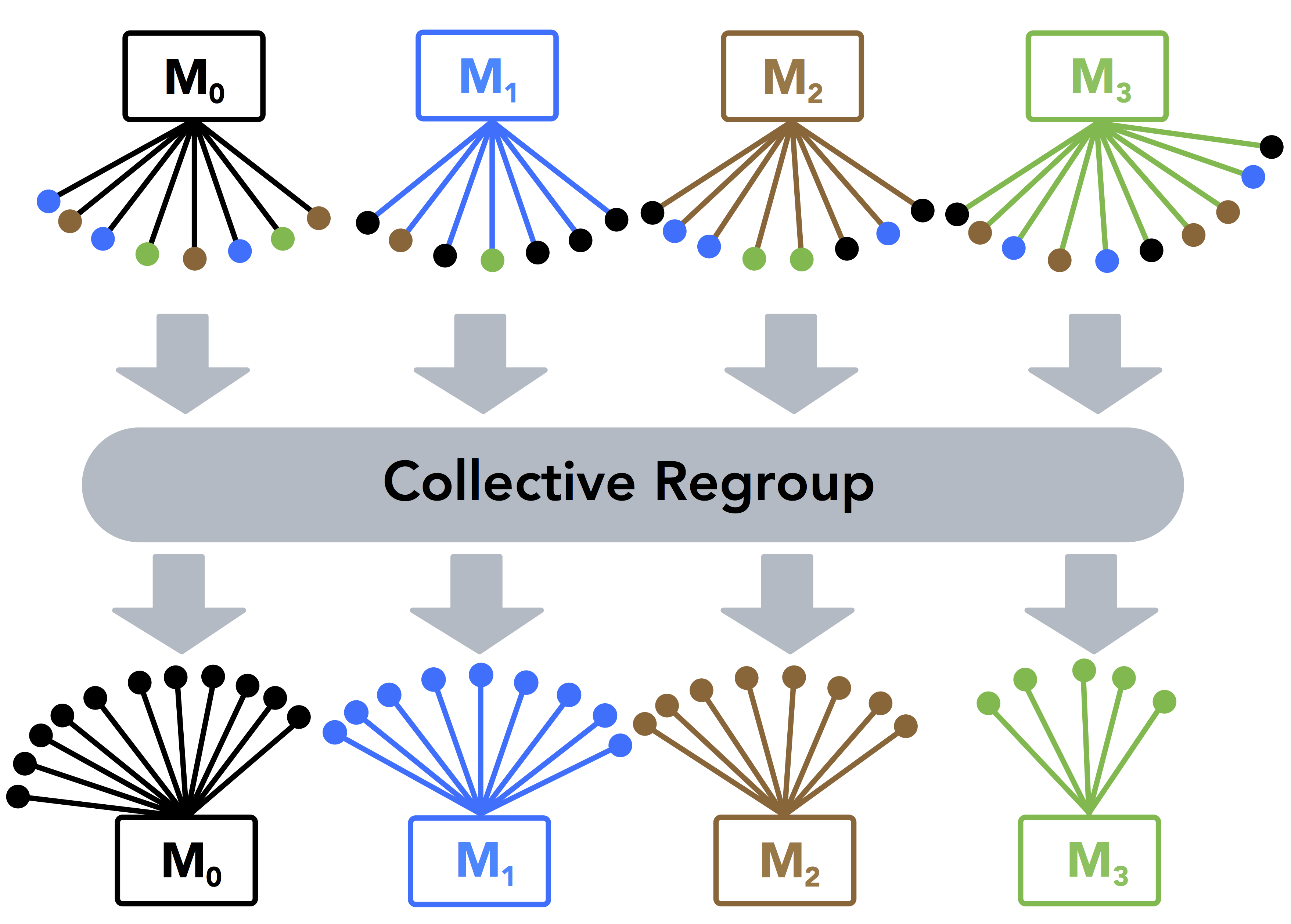
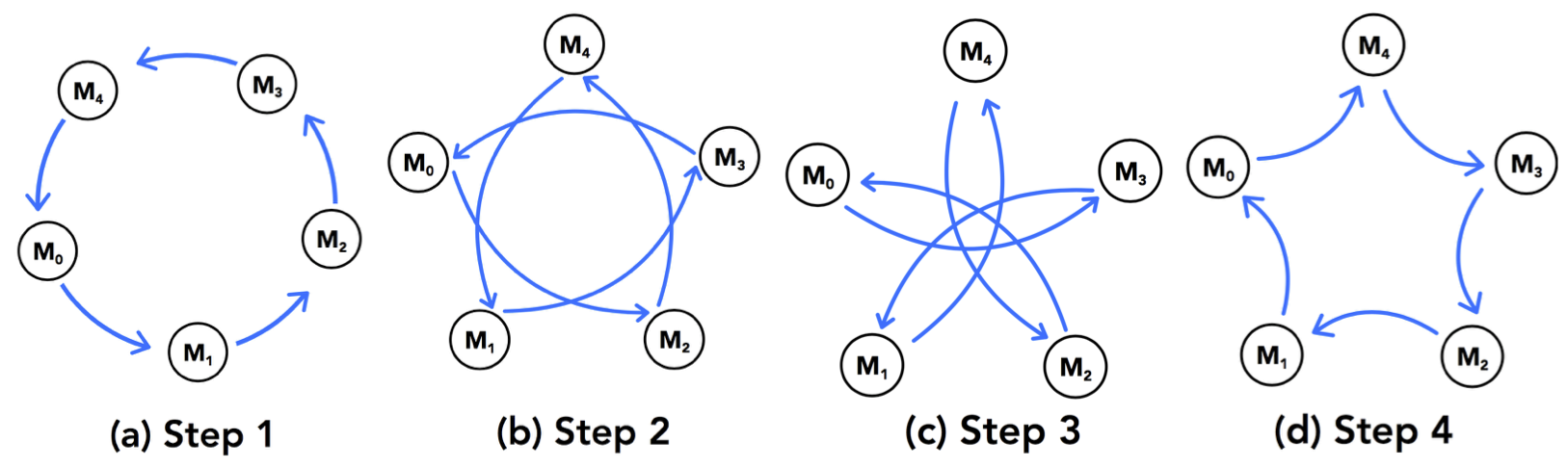
and the classic “AlltoAll” communication pattern is decoupled to s steps, where each step conducts a partial collective communication among selected mappers following a user-defined order.
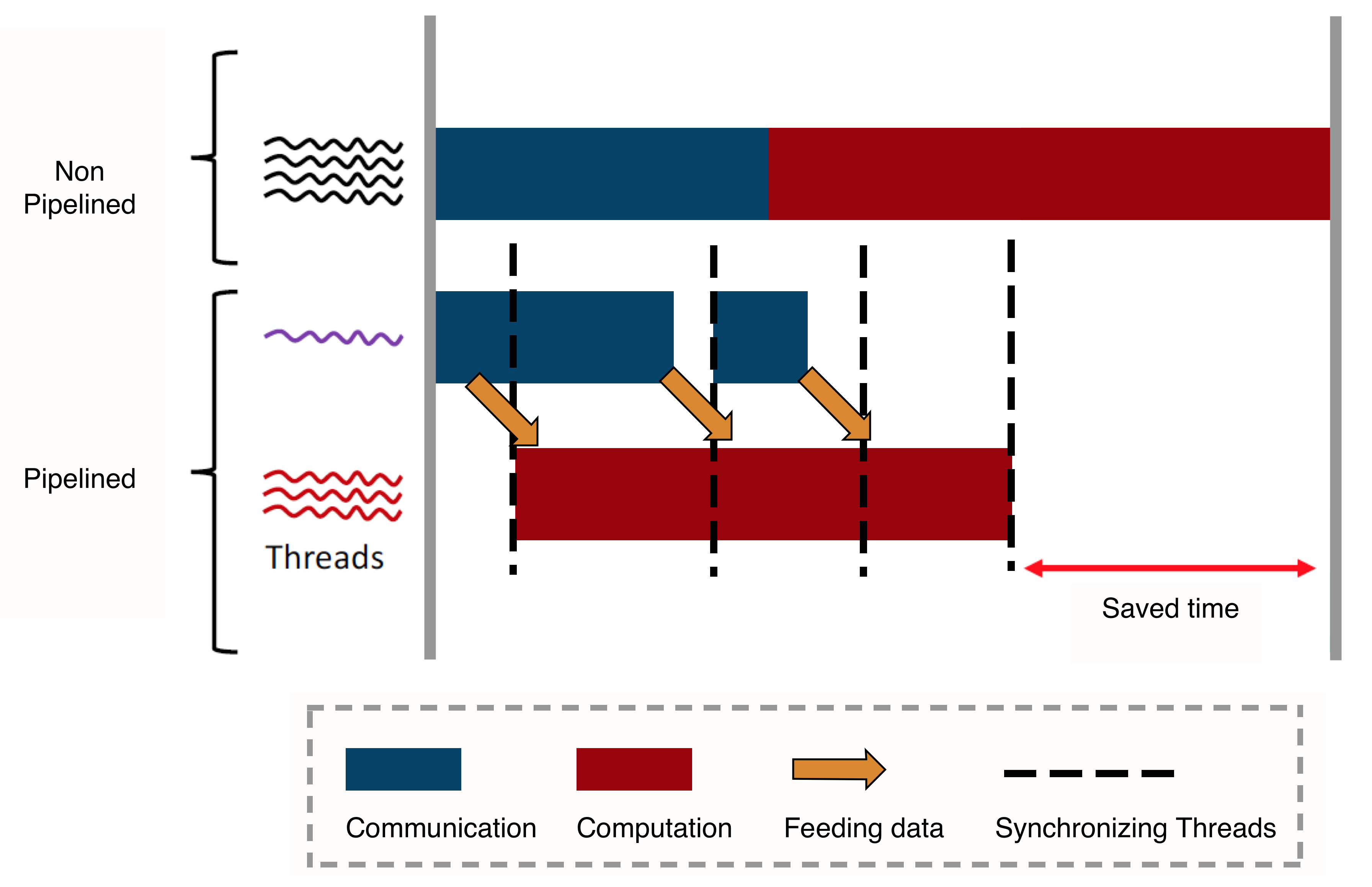
Because of this decoupling of communication, the communication is able to be interleaved by local computation in a pipeline design
Single-Node Load Balancing
At intra-node level, Harp-DAAL-Subgraph applies a neighbour list partitioning technique to the computation of counts for each vertex of input graph. This technique alleviates the ill load balancing problem due to the irregularity of data distribution of the input graph.
Code Walk-Through
The code of harp-daal-subgraph is located at here. The body of implementation is within the SCDaalCollectiveMapper.java file that invokes the native DAAL kernels via Java API
import com.intel.daal.algorithms.subgraph.*;
It takes the following steps in runSC function to finish the whole counting task
Read in Data from HDFS
...
// read in template data
HomogenNumericTable[] file_tables = load_data_names(vFilePaths);
Distri scAlgorithm = new Distri(daal_Context, Double.class, Method.defaultSC);
scAlgorithm.input.set(InputId.filenames, file_tables[0]);
scAlgorithm.input.set(InputId.fileoffset, file_tables[1]);
scAlgorithm.input.readGraph();
...
//initialize daal graph structure
scAlgorithm.input.initGraph();
...
// read in template data
HomogenNumericTable[] t_tables = load_data_names(tFilesPaths);
scAlgorithm.input.set(InputId.tfilenames, t_tables[0]);
scAlgorithm.input.set(InputId.tfileoffset, t_tables[1]);
scAlgorithm.input.readTemplate();
scAlgorithm.input.initTemplate();
Both of input graph data and template data are loaded directly into native memory space of DAAL kernels from HDFS filesystem.
The local computation and communication codes are located at file colorcount_HJ.java, where the function do_full_count is invoked by
full_count = graph_count.do_full_count(numIteration);
The main body of do_full_count has the following structure
// looping all the iterations
for(int cur_itr = 0; cur_itr < this.num_iter; cur_itr++)
{
...
// looping over all the sub-templates in a reverse order
for( int s = this.subtemplate_count -1; s > 0; --s)
{
// local computation
...
// inter-node communication
...
}
...
}
Computation
The local computation will detect the position and shapes of sub-templates and compute the counting values contributed by local neighbours of each graph vertex.
if( this.num_verts_sub_ato == 1)
{
// if the subtemplate size == 1
if ( s == this.subtemplate_count - 1)
{
this.scAlgorithm.input.initDTSub(s);
this.scAlgorithm.computeBottom(s);
}
else
this.scAlgorithm.input.setToTable(this.subtemplate_count - 1, s);
}else
{
// if the subtemplate has a size > 1
this.scAlgorithm.input.initDTSub(s);
scAlgorithm.computeNonBottom(s);
}
The computation follows a dynamic programming technique, where the computation of sub-template s==k uses the results from sub-template s<k.
Communication
If the program is running on more than one mappers and the template has more than one vertex, there comes the inter-node communication after finishing the computation
if (this.mapper_num > 1 && this.num_verts_sub_ato > 1)
{
...
regroup_update_pipeline(s);
...
}
Running the codes
Make sure that the code is placed in the /harp/experimental directory.
Run the harp-daal-subgraph.sh script here to run the code.
cd $HARP_ROOT/experimental
./test_scripts/harp-daal-subgraph.sh
The details of script is here