Implicit Alternating Least Squares

Alternating least squares (ALS) is an algorithm used in recommender systems, which trains the model data X and Y to minimize the cost function as below



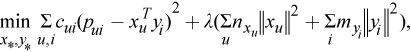
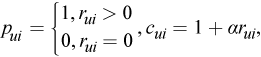
where

  • c_ui measures the confidence in observing p_ui
  • alpha is the rate of confidence
  • r_ui is the element of the matrix R
  • labmda is the parameter of the regularization
  • n_xu, m_yi denote the number of ratings of user u and item i respectively.

ALS alternatively computes model x and y independently of each other in the following formula:





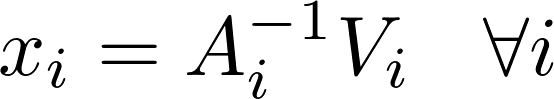
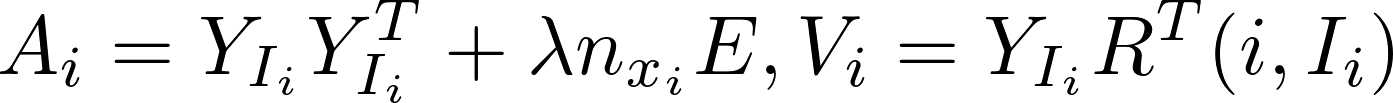
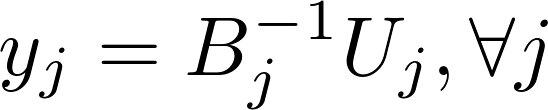
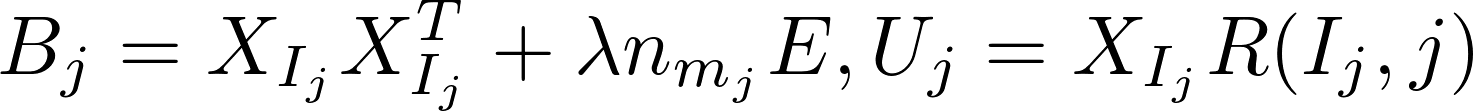
Harp-DAAL currently supports distributed mode of ALS 12 for dense and sparse (CSR format) input datasets.

More algorithmic details from Intel DAAL documentation is here.

  1. Rudolf Fleischer, Jinhui Xu. Algorithmic Aspects in Information and Management. 4th International conference, AAIM 2008, Shanghai, China, June 23-25, 2008. Proceedings, Springer. [return]
  2. Yifan Hu, Yehuda Koren, Chris Volinsky. Collaborative Filtering for Implicit Feedback Datasets. ICDM’08. Eighth IEEE International Conference, 2008. [return]