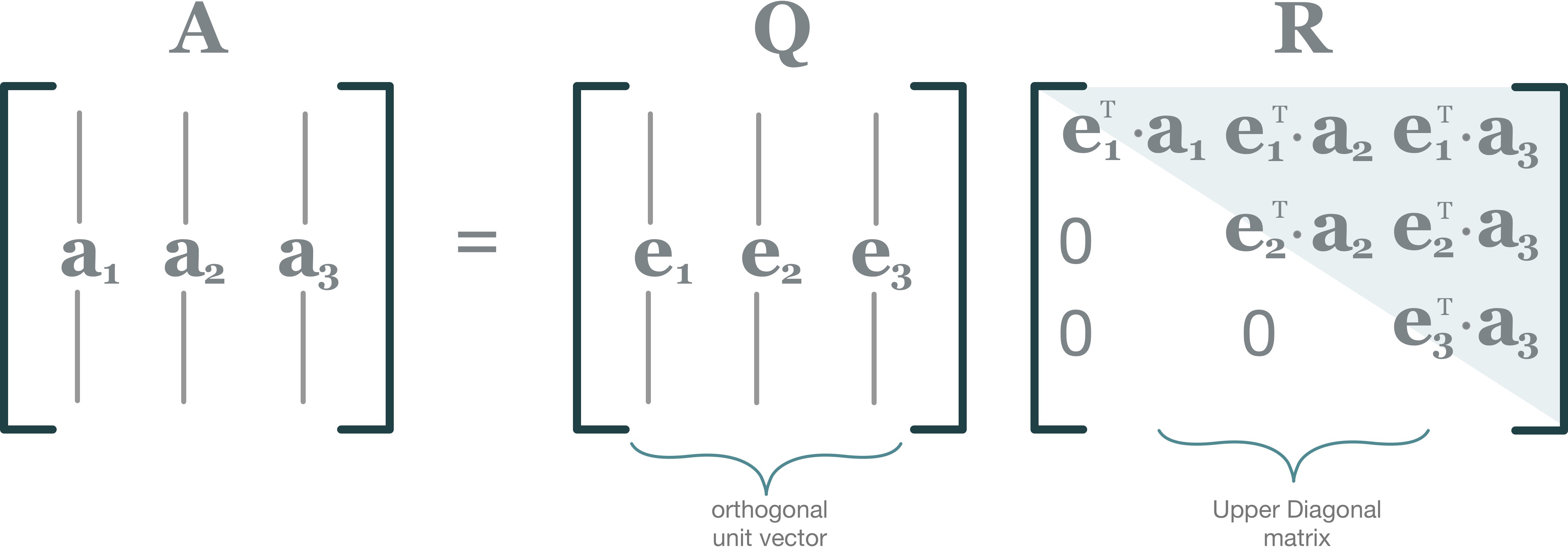
The QR decomposition or QR factorization of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. A QR decomposition of a real square matrix A is a decomposition of A as A = QR, where Q is an orthogonal matrix (its columns are orthogonal unit vectors meaning QTQ = I) and R is an upper triangular matrix (also called right triangular matrix).
Harp-DAAL currently supports distributed mode of QR for dense input datasets.
More algorithmic details from Intel DAAL documentation is here.